공개키 암호화 방식
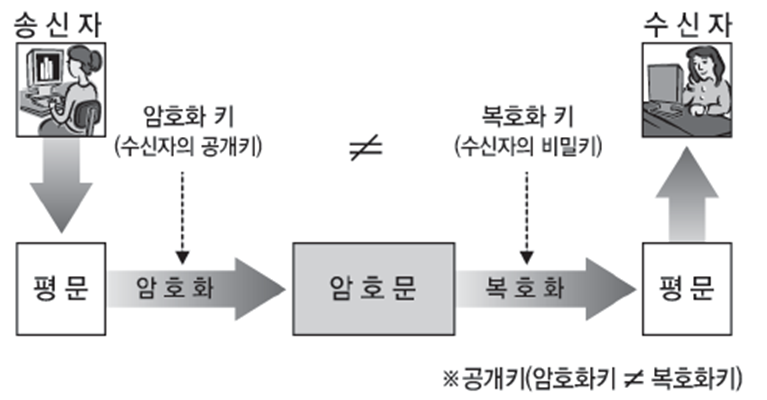
1976년 디페(Diffie)와 헬만(Hellman)에 의해 공개키 암호화 방식의 개념이 도입되었다.
암호를 위해 개인키와 공개키로 이루어진 한 쌍의 키를 생성하는데
개인키는 소유자만이 간직하고 공개키는 외부에 필요한 사람에게 배포한다(암호화 키와 복호화 키는 달라야함).
공개키 암호 방식의 장점
-키의 안전한 분배 문제와 키 관리 문제가 용이하다.
-간단하게 신원 확인이 가능하다.
공개키 암호 방식의 단점
-대칭키 암호 알고리즘보다 암호화를 위한 키의 크기가 상대적으로 크다.
-암호화 및 복호화를 위한 처리 속도가 대칭키 암호 방식보다 느리다.
인수분해(integer factorization) 문제 기반 알고리즘
RSA 알고리즘
RSA 알고리즘이란 Rivest, Shamir, Adleman 이 세사람이 만든 알고리즘이다(앞글자를 따서 RSA).
이 알고리즘을 알아보기 전 우리가 알아야 할 정보가 두가지 있다.
1. K+(K-(m)) = m
공개키로 암호화한 정보를 개인키로 복호화를 한다면 평문이 나와야한다.
k+() : 공개키
k-() : 비밀키
m : 평문
보통 K+(m) = c 라 칭함.
2. 공개키로 개인키를 유추할 수 없어야한다.
공개키는 공개되어있기때문에 만약 개인키를 쉽게 유추할 수 있다면 보안이 쉽게 뚫리게 된다.
+ 만약 자신의 개인키로 암호화 한 뒤 상대방한테 전달하면 안전할까?
예를들어 Bob과 Alice 가 통신을 한다고 하자
만약 Alice가 자신의 개인키로 암호화 한 Ka-(m)을 Bob에게 넘기면 어떤 문제가 발생할까
위에서 K+(K-(m))이라 하였는데 이를 K-(K+(m))와 같이 반대로 해도 같은 결과가 나오게 된다(수학적 이론에 기반).
보통 해커들이나 네트워크 관리자들은 통신 내용을 볼 수 있는데(스니핑)
Ka+()는 공개가 되어 있으므로 Ka-(m)을 탈취하여 이를 복호화한 뒤 m을 볼 수 있게된다.
그러므로 이 방식은 위험하다(전자서명할 때 사용하기는 함).
RSA 암호화의 진행과정
키 값 결정
1. 2개의 아주 큰 소수 p, q 를 선택한다(약 1024비트 정도).
2. n = pq, z = (p-1)(q-1) 를 정의한다.
3. z와 서로소인 e를 정의한다(e 값이 작을수록 연산속도가 증가한다).
이를 수학적 기호로 작성하면 gcd(e,z) = 1
4. ed mod z = 1 or ed ≡ 1(mod z)인 d를 결정한다.
ed mod z = 1 ?
ed - 1 이 z로 나누어 떨어진다는 뜻으로, 이를 정수론에서 합동이라고 한다(뒤에 식으로도 표현 가능).
또한 양변(ed와 1)을 z로 나누었을 때 나머지가 같다고 이해해도 된다.
5. 공개키는 K+(n,e) 가 되고 비밀키는 (n,d)가 된다.
암호화 & 복호화
암호화 : c = m^e mod n
m^e 를 n으로 나눈것이 c가 됨
복호화 : m = c^d mod n
c^d 를 n으로 나눈것이 c가 됨
이때 m = (m^e mod n)^d mod n 이 되는데 이유가 궁금하다면 뒤에 나올 심화과정을 확인하자.
예시) 키 값 결정
1. p = 5, q = 7로 결정한다.
2. 그러면 n = 35, z = 24가 된다.
3. e = 5 로 선택.
4. ed ≡ 1(mod z) 인 d = 29 결정 ( ed ≡ 1(mod z) ≫ 29 x 5 - 1 = 144, 이때 144는 24로 나누어떨어진다)
예시) 암호화
문자 l 을 암호화한다고 했을 때
m = 12가 된다(12번째 문자).
m^e = 1524832 가 되고
c = m^e mod n 이므로 c = 17이 된다.
예시) 복호화
c = 17 이므로
c^d = 481968572106750915091411825223071697 가 된다.
m = c^d mod n 이므로 m = 12 가 나온다.
+ 페르마의 소정리
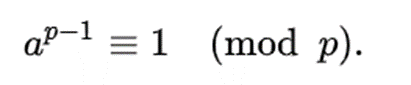
만약 p 가 소수이고 p와 서로소인 a가 있을 때 위에 식이 무조건 성립한다는 정리이다. 이를 예시로 알아보자.
a = 2 이고 p = 5 라고 가정하면 a^(p-1) = 2^4 = 16이 되고 이를 5로 나누게 되면 1이 나머지가 된다.
이 정리는 p와 a가 조건만 만족하면 어떤 식이든 성립한다.
+ 오일러 정리
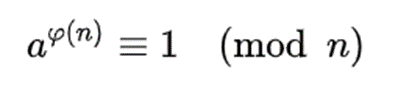
오일러 정리는 페르마의 소정리를 확장한것이다.
만약 a와 n이 서로소이면 위에 식이 성립한다는 정리이다.
이때 φ(n)은 n보다 작은 양수 중 n과 서로소인 숫자의 개수이다.
예시로 φ(6) = |{1,5}| = 2가 된다.
또한 6 = 2 x 3 이므로 φ(6) = (2-1)(3-1) = 2라고도 할 수 있다.
n = pq 이면 φ(n) = (p-1)(q-1)
n = p(소수) 인 경우
φ(p) = |{1,2,3,4,···,p-1}| = p-1이 되는데 이를 오일러 정리에 넣으면 페르마의 소정리가 나오게 된다.
이제 이러한 개념을 통해 암호화와 복호화 과정을 자세히 이해해보자.
+ 암호화 복호화의 심화 이해
1. 만약 n =p 이면 φ(n) = p-1이고 → 페르마의 소정리
n = pq 이면 φ(n) = (p-1)(q-1)이다.
2. a와 n이 서로소이면 a^(p-1)(q-1) ≡ 1 mod n(=pq)이다.
3.ed ≡ 1 mod z(= (p-1)(q-1))
수학 기호로 z | ed -1이라 적는데 이는 좌변이 우변을 나누었을 때 나누어떨어진다는 의미이다.
4. ed - 1 = kz, ed = k(p-1)(q-1) + 1
ed -1 이 z 로 나누어떨어진다는것은 ed - 1 이 z의 정수배임을 나타낸다.
5. c = a^e mod n이므로 평문 m = c^d mod n = a^ed mod n 이 된다.
6. 4번에 의해 a^{k(p-1)(q-1)+1} mod n 이 되고 a를 밖으로 꺼내서
a x {a^(p-1)(q-1) mod n }^k mod n 로 쓸 수 있다.
7. a^(p-1)(q-1) mod n = 1이므로(합동) 결국 a가 된다.
RSA는 진짜로 안전한가?
공개키가 (n,e) 이고 비밀키가 (n,d)인데 공개키는 이미 공개가 되어있으므로
이 암호문을 뚫는 핵심 요소는 d값을 찾는것이다.
이 d 값을 찾으려면 위에서 알아본대로 정수방정식 ed ≡ 1(mod z)를 풀어야하는데 이를 푸는것은 그렇게 어렵지 않다.
그렇다면 왜 아직도 RSA가 쓰일만큼 안전할까?
정답은 공격자가 z를 모르기때문에 암호문이 뚫리지 않는것이다.
우리들은 p와 q를 알기때문에 n과 z를 쉽게 알 수 있지만 공격자는 p 와 q를 몰라서 z를 알기가 매우 까다로워진다.
또한 소인수분해로 알아내면 되는것이 아닌가? 라고 물을수 있지만
p와 q는 매우 큰 소수이기 때문에 이를 현존하는 가장 빠른 컴퓨터로 돌려도 죽을때까지 알 수 없다.
하지만 만약 양자컴퓨터가 개발된다면 깨질수도..?
기타 공개키 암호 방식
ElGamal
이산 수학 계산을 요구함
장점 : 데이터에 대한 암호화와 전자서명에 사용 가능
단점 : 다른 공개키 방식보다 암호문의 길이가 2배로 늘어남
ECC(Elliptic Curve Cryptography)
엘가말 암호에서 사용하는 곱셈군을 타원곡선의 덧셈군으로 대치하는 방식
전자서명, 비밀키의 안전한 분배와 관리, 무선통신, 서명, 인증 등 빠른 속도와 제한된 대역폭 등이
요구되는 무선통신 분야에서 특히 유용
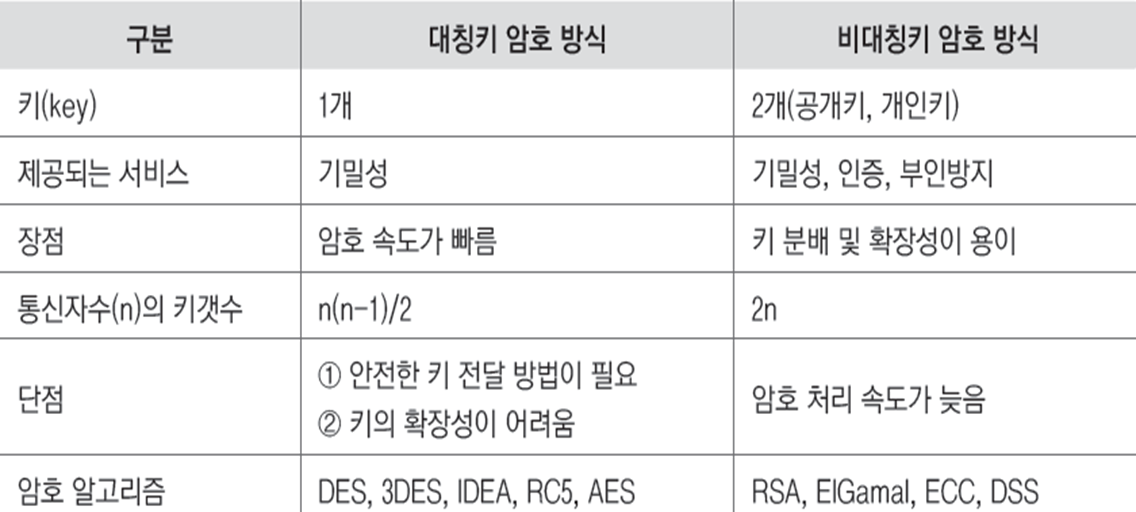
대칭키 VS 비대칭키 암호 방식
'암호학' 카테고리의 다른 글
| [암호학] 암호화 기반 인증기술 (1) | 2024.10.30 |
|---|---|
| [암호학] 키 관리와 해쉬 함수 (1) | 2024.10.29 |
| [암호학] DES란? (1) | 2024.10.25 |
| [암호학] 대칭키 암호화 방식 (1) | 2024.10.22 |
| [암호학] 암호학의 역사 (1) | 2024.10.20 |



