[암호학] 정수론

정수론

정수론은 정수를 연구하는 분야이다.
 
정수론을 왜 배우는지 궁금해할수 있는데
 
우리가 현대 암호를 이해하려면 정수론을 필히 알고있어야한다.
 
그러므로 한번 같이 알아보자.
 

Division(나누기)

지금부터 나오는 수들은 모두 정수이다.

 
이 쉬운 나누기를 왜 배우냐고 할 수 있는데 
 
정수론에선 중요하기때문에 짚고 넘어가도록 하겠다.
 
일반적으로 b를 a로 나눌때(나누어 떨어짐) a와 b의 관계는

$$ b=ac (c는 상수) $$

 
가 된다(b는 a의 배수). 
 
또한 a는 b의 약수라고 할 수 있다.
 
이 a와 b의 관계를 정수론에선 

$$ a\ |\ b $$

 
로 칭한다.
 
또한 몇가지 공식이 있는데

a | b 이고 a | c 이면 a | (b+c) 이다.
ex) 3 | 6 이고 3 | 9 이면 3 | 15이다.

a | b이면 모든 c에 대해서 a | bc이다.
ex) 5 | 10이면 5 | 20, 5 | 30, 5 | 40, ...

a | b 이고 b | c이면 a | c 이다.
ex) 4 | 8이고 8 | 24면 4 | 24이다.

 

Division Algorithm

a와 d를 나눌때 몫을 q라고 하고 나머지를 r이라고 하면
 
$a=dq+r$
 
로 표현된다.
 
이때 a, q, r는 정수, d는 양의 정수이며 r의 범위는 0 ≤ r < d 이다.
 
ex) $17=5\cdot3+2$ 에서 0 ≤ 2 < 5를 만족함을 알 수 있다.
 
그렇다면 -11을 3으로 나누게 되면 나머지가 몇일까?
 
$-11=3\cdot(-3)-2$  또는 $-11=3\cdot(-4)+1$ 둘중에 하나인데 정답은 후자이다.
 
나머지의 범위를 생각해보면 전자는 0 ≤ -2 < 3 으로 만족하지않고
 
후자는 0 ≤ 1 < 3 으로 만족하는것을 볼 수 있다.

Prime(소수)

소수란 다들 알겠지만 약수로 1과 자기자신만 가지는 수를 뜻한다.
 
또한 1보다 크고 소수가 아닌 수는 composite(합성수)라고 한다.
 
소인수분해는 모든 양의 정수들을 소수의 곱으로 나타내는것인데
 
이 소인수분해 방법은 한가지로 유일하다.
 
ex) $20$은 $ 2^{2}\times 5$  인데 이 이외의 경우의 수는 존재하지 않는다.
 

Greatest Common Divisors(최대공약수)

최대공약수를 알아보기전에 먼저 공약수에 대해서 먼저 알아보자.
 
어떤 두 수의 공통된 약수를 바로 공약수라고 한다.
 
12의 약수는 1, 2, 3, 4, 6, 12이고 8의 약수는 1, 2, 4, 8인데 이중 공약수는 1, 2, 4이다.
 
이때 최대공약수는 공약수중 가장 큰 수를 말하며 12와 8의 최대 공약수는 4이다.
 
이를 수학적 기호로 작성하면 $gcd(a,b)$라고 한다.
 

소수로 최대공약수 나타내기

$a={p_{1}}^{a_{1}}{p_{2}}^{a_{2}}...{p_{n}}^{a_{n}},b={p_{1}}^{a_{1}}{p_{2}}^{a_{2}}...{p_{n}}^{a_{n}}$ 라고 하면( 이때 ${p_{1}}<{p_{2}}<...<{p_{n}}$이다. )
 
$gcd(a,b)=p{_{1}}^{min(a_{1},b_{1})}p{_{2}}^{min(a_{2},b_{2})}...p{_{n}}^{min(a_{n},b_{n})}$ 가 된다.
 

Examples

 
$a=60=2^{2}3^{1}5^{1}$
$b=54=2^{1}3^{3}5^{0}$
$gcd(a,b)=2^{1}3^{1}5^{0}=6$
 

Relatively Prime or Coprime(서로소) 

아까 우리가 최대공약수를 알아보았는데
 
만약 정수 a,b에 대해서 $gcd(a,b)=1$이라면 이를 서로소라고 한다.
 
또한 3개 이상의 정수에 대하여 아무거나 뽑은 두가지 정수가 모두 서로소라면 이를 pairwise relatively prime(쌍마다 서로소)라고 한다.
 

Examples

15, 17, 28은 쌍마다 서로소인가?
-> $gcd(15,17)=1$, $gcd(15,28)=1$, $gcd(17,28)=1$ 이므로 쌍마다 서로소이다.
 

Least Common Multiples(최소공배수)

이번에도 최소공배수를 알아보기 전에 공배수를 먼저 알아보자.
 
어떤 두 수의 공통된 배수를 바로 공배수라고 한다.
 
5의 배수는 5, 10, 15, 20, 25... 이고 6의 배수는 6, 12, 18, 24, 30 ...인데 이중 공배수는 30이다.
 
이때 최소공배수는 공배수중 가장 작은 수를 말하며 5와 6의 최소 공배수는 30이다.
 
이를 수학적 기호로 작성하면 $lcm(a,b)$라고 한다.
 

소수로 최소공배수 나타내기

$a={p_{1}}^{a_{1}}{p_{2}}^{a_{2}}...{p_{n}}^{a_{n}},b={p_{1}}^{b_{1}}{p_{2}}^{b_{2}}...{p_{n}}^{b_{n}}$ 라고 하면( 이때 ${p_{1}}<{p_{2}}<...<{p_{n}}$이다. )
 
$lcm(a,b)=p{_{1}}^{max(a_{1},b_{1})}p{_{2}}^{max(a_{2},b_{2})}...p{_{n}}^{max(a_{n},b_{n})}$ 가 된다.
 

Examples

$a=60=2^{2}3^{1}5^{1}$
$b=54=2^{1}3^{3}5^{0}$
$lcm(a,b)=2^{2}3^{3}5^{1}=540$
 

GCD와 LCM의 관계

$a=60=2^{2}3^{1}5^{1}$
$b=54=2^{1}3^{3}5^{0}$
 
에서 
$gcd(a,b)=2^{1}3^{1}5^{0}=6$
$lcm(a,b)=2^{2}3^{3}5^{1}=540$
 
이를 자세히보면 gcd와 lcm이 a,b를 이루고있으므로
 
$a\times b=gcd(a,b)\times lcm(a,b)$ 가 되는것을 알 수 있다.
 

Modular 연산

이 연산은 아마 익숙하지 않을것이다.
 
modular은 파이썬의 %연산자라고 이해하면 편하다(C언어와는 차이가 있는데 C언어의 %는 나머지로 음수를 출력한다)
 
기호로 $mod$라고 하는데
 
$ a\ mod\ m$은 a를 m으로 나누었을 때 나머지를 뜻한다.
 

Examples

$ 9\ mod\ 4=1$
$ 9\ mod\ 3=0$
$ 9\ mod\ 10=9$
$ -13\ mod\ 4=3$
 

Congruences(합동)

$a\equiv b\ (mod\ m)$처럼 mod가 식 밖으로 나올수도 있는데
 
이 뜻은 좌변 a를 m으로 나눈 나머지와 우변 b를 m으로 나눈 나머지가 같다는것이다.
 
예로 $11\equiv 1\ (mod\ 10)$이므로 11과 1은 합동이라고 할 수 있다.
 
또한 이 예시에서 $a-b=11-1=10$이므로 $ m| a-b $으로도 표현가능하다(좌변과 우변을 빼서 m으로 나누어 떨어진다면 합동이라고 이해하자).
 

Examples

$46\equiv 68\ (mod\ 11)$이 참인가?
-> $ 11| (46-68) $이므로 참이다.

$46\equiv 68\ (mod\ 22)$이 참인가?
-> $ 22| (46-68) $이므로 참이다.

$z\equiv 12\ (mod\ 10)$이 되는 모든 정수 z를 찾으시오
-> ${...-28, -18, -8, 2, 12, 22, 32, ...}$
 

동치

$a\equiv b\ (mod\ m)$는 $a = b +km$인 $k$가 존재한다는 말과 동치이다.
 
$ m\ |\  a-b $ 는 결국 우변이 좌변의 배수 형태라는것을 의미한다. $a - b = km$
 
이를 a에 대한 식으로 정리하면 $a = b +km$가 나오게된다.
 

Congruence의 성질

$a\equiv b\ (mod\ m)$이고 $c\equiv d\ (mod\ m)$이면
 
$a+c\equiv b+d\ (mod\ m)$이고 $ac\equiv bd\ (mod\ m)$이다.
 
증명은 위에 나온 동치를 사용하여 증명할 수 있다(스스로 한번 해보자!).
 
 
또한 $ x^{n}\ mod\ m=(x\ mod\ m)^{n}$ 이다(이 모양 어디서 본적 있지 않나?).
 
이 둘의 차이는 큰데
 
$ x^{n}$ 이 아주 큰 수라고 가정하면(n이 큼)
 
앞의 식은 아주 큰 수를 나눈다는 뜻이 된다.
 
컴퓨터는 아주 큰 수를 나누게되므로 작동이 현저히 느려지게된다.
 
하지만 뒤의 식은 작은 상태에서 나눈 뒤 제곱하므로
 
 오버플로우가 발생하지 않게된다.
 

항등원과 역원

 
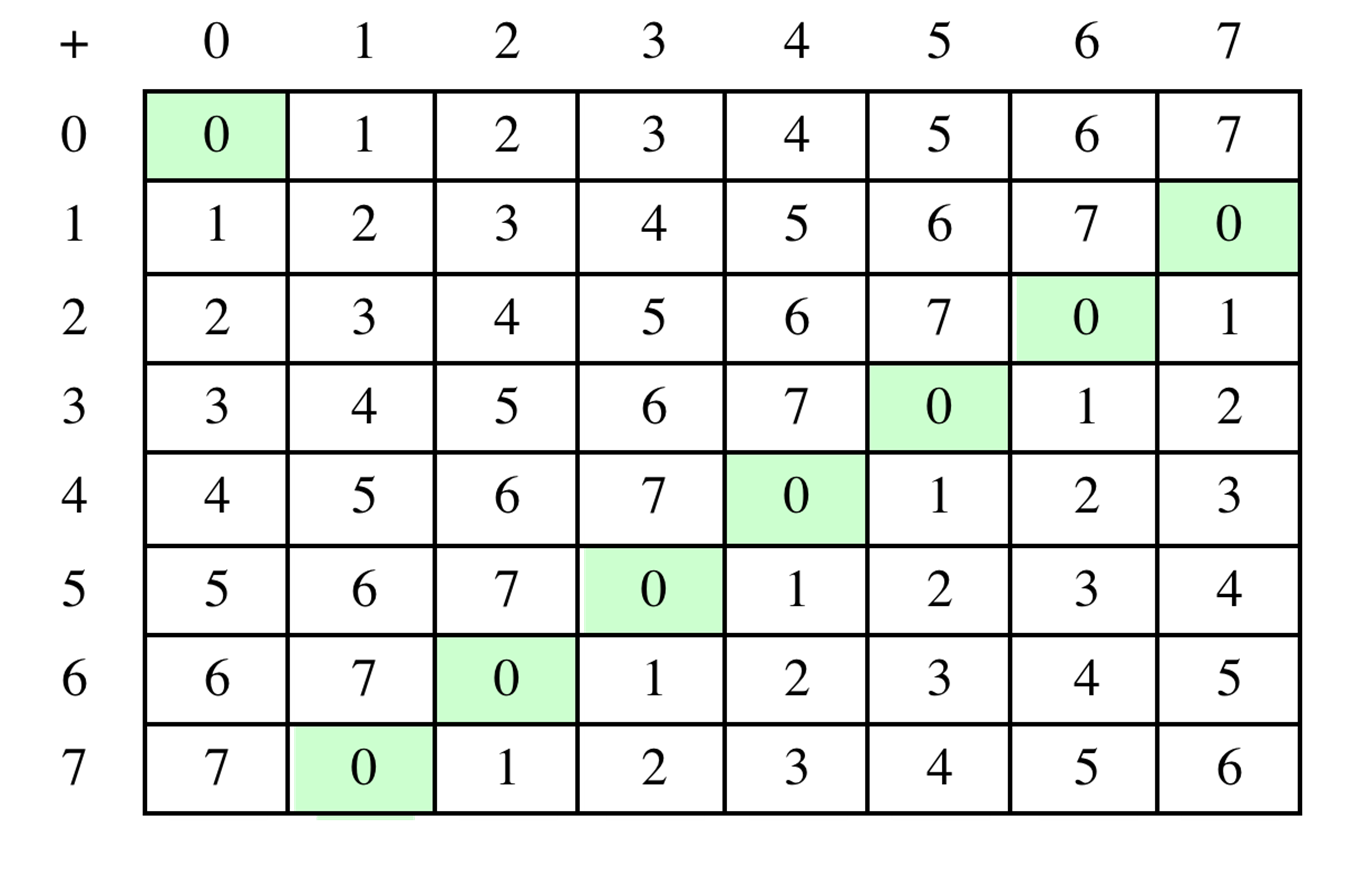
이 사진은 행과 열을 더한 값을 $mod\ 8$ 연산을 하는것이다.
 
이때 0에만 색칠이 되어있는것이 보이는가?
 
0은 더하기 계산에서 항등원을 뜻한다.
 
항등원이란 어떤 수에 특정 연산을 했을때 자기 자신이 나오도록 하는 원소이다.
 
또한 항등원이 나오도록 하는 원소를 역원이라 한다.
 
예로 2의 역원은 6이며 3의 역원은 5이다.
 

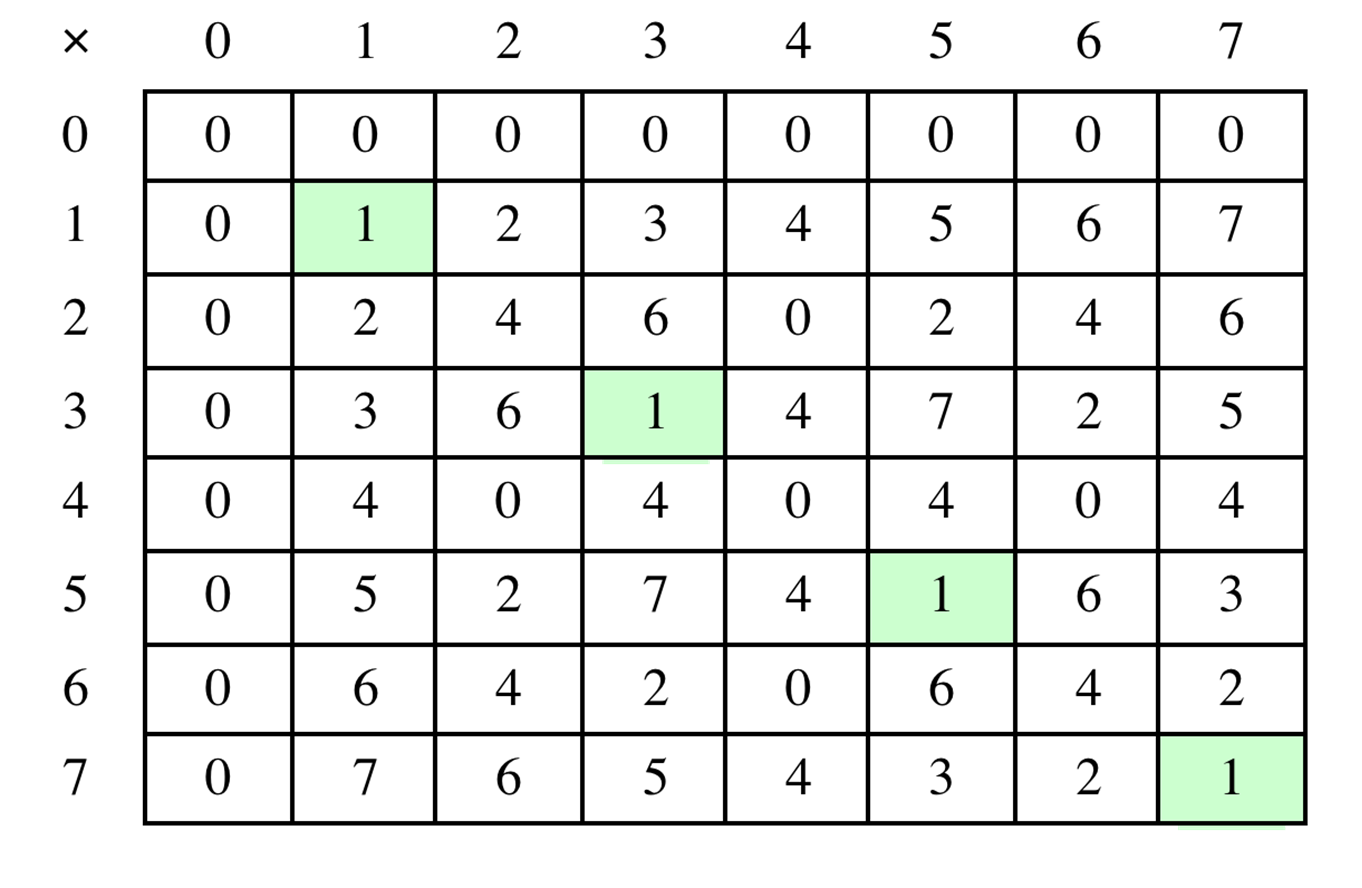
이 사진은 행과 열을 곱한값을 $mod\ 8$ 연산을 하는것이다.
 
곱에서 항등원은 1인데 앞의 사진에서는 모든 항에 항등원이 나왔지만
 
이 사진에선 띄엄띄엄 나오는것을 볼 수 있다.
 
이것이 문제인 이유는 방정식을 풀면서 역원이 필요한 경우가 있는데
 
저 사진에서 3에대한 역원은 3으로 존재하지만 2에 대한 역원은 존재하지 않는다.
 
고로 방정식을 풀지못하는 경우가 나올수도 있다는 뜻이다.
 

$Z_{n}$에서 성립하는 성질

$Z_{n}$이란 무한대의 정수를 n으로 나누었을 때 나머지들의 집합을 의미한다.
 
이 $Z_{n}$에서는 다음과 같은 성질이 존재한다.
 
교환법칙
$(w+x) mod\ n = (x+w) mod\ n  $
$(w\times x)mod\;n=(x\times w)mod\;n$
 
결합법칙
$[(w+ x)+ y]mod\;n=[w+(x+ y)]mod\;n$
$[(w\times x)\times y]mod\;n=[w\times(x\times y)]mod\;n$
 
분배법칙
$[w\times(x+y)]mod\;n=[(w\times x)+(w\times y)]mod\;n$
 
항등원
$(0+w) mod\ n = w\ mod\ n  $
$(1\times w) mod\ n = w\ mod\ n  $
 
역원
덧셈의 경우에는 항상 존재하지만 역원의 경우에는 존재할수도 있고 없을수도 있다(n에따라 다름).
 

Euclidean Algorithm

유클리드 호제법이란 두 정수의 최소공배수를 구하는 아주 빠른 알고리즘이다.
 
이번에는 예시를 먼저 보고 함께 알아보도록 하자.
 
먼저 우리의 목표는 $gcd(287,91)$을 구하는것이다.
 
이를 위해서 먼저 큰 수를 작은수로 나눈다.
 
그러면 $287 = 91\cdot 3 + 14$이 된다.
 
이때 $gcd(287,91)=gcd(91,14)$가 되서
 
이를 같은방법으로 하면
 
$91=14\cdot 6+7$ 이 되고
 
$gcd(91,14)=gcd(14,7)$이므로
 
$14=7\cdot 2+0$, 결국
 
$7\ |\ 14$이므로 $gcd(14,7) = 7$임을 알 수 있다.
 
그러므로 $gcd(287,91) = 7$이다.
 
무려 나누기 2번으로 답을 구했다!
 
지금까지 유클리드 호제법을 이용하여 답을 구해보았다.
 
이제 원리에 대해 공부해보자

Euclidean Algorithm의 원리

이 유클리드 호제법의 핵심은 

 

$a\ >\ b$일때 $a = qb+r$에서 

 

$gcd(a,b) = gcd(b,r)$인것이다.
 

만약 $gcd(a,b) = c$라고 가정하자.

 

$r = a - qb$로 놓을수있는데 

 

이때 $c$는 $a,b$의 약수가 된다.

 

그러므로 각각 $a = ct$, $b = cs$로 나타낼 수 있다.

 

이를 r에 대한 식에 넣으면 

 

$r = ct - qcs = c(t-qs)$로 표현된다.

 

식의 형태에 따라 $r$은 $c$의 배수임을 알 수 있다( $c\ |\ r$ ).

 

그래서 $c$는 $r$의 약수이면서 $b$의 약수이기 때문에 $ c\leq gcd(b,r)$이라는 결론이 나온다

($c$는 최대공약수이거나 그보다 작은 약수이다).

 

다음으로  $gcd(b,r) = d$라고 가정하자.

 

위에처럼 해보면 $d\ |\ a$임을 쉽게 알 수 있다(스스로 한번 해보자).

 

그래서 $d$는 $a$의 약수이면서 $b$의 약수이기 때문에 $ d\leq gcd(a,b)$이라는 결론이 나온다.

 

이때 $ c\leq gcd(b,r)$에서 $gcd(b,r) = d$이므로 $c\leq d$이고

 

$ d\leq gcd(a,b)$에서 $gcd(a,b) = c$이므로 $d\leq c$가 되는데 이를 만족하는 경우는

 

$c = d$인 경우, 즉 $gcd(a,b) = gcd(b,r)$이다.

 

$ \therefore gcd(a,b) = gcd(b,r)$

Extended Euclidean Algorithm

앞에서 본 호제법은 최대공약수를 찾는것까지만 했다면

 

확장된 호제법은 

 

$ax + by = d = gcd(a,b)$란 식이 있을때 $x$와 $y$를 찾는 정수방정식을 풀어준다.

 

이때 알아야할것이 정수방정식은 무조건 답이 존재하는것은 아니다.

 

ex) $10x + 26y = 1$(좌변은 짝수항이고 우변은 홀수항이라 답이 존재하지 않는다.)

 

그래서 정수방정식이 답이 있으려면

 

위에 있는 $d$가 $a$와 $b$의 최대공약수이거나 그 배수인 경우여야한다(작으면 X).

 

이제 예시와 함께 자세하게 알아보자.

 

Extended Euclidean Algorithm의 예시

문제 : $125x + 23y = 1$을 만족하는 $(x, y)$를 찾으시오

 

먼저 유클리드 알고리즘을 돌리면

 

$1)\ 125 = 23 \times 5 + 10$

 

$2)\ 23 = 10 \times 2 + 3$

 

$3)\ 10 = 3 \times 3 + 1$  

 

이므로 $gcd(125,23) = 1$임을 알 수 있다.

 

이제 이 식들을 활용해서 필요없는 숫자들을 소거시킬것이다.

 

이때 필요없는 숫자란 각 항들의 나머지들을 말한다(마지막으로 나온 나머지는 최대공약수이므로 필요하다)

 

먼저 3을 없애보자.

 

2번 식에서 양변에 3을 곱하고( $23 \times 3 = 10 \times 6 + 3 \times 3$ )

 

3번 식에서 1을 좌변으로 옮긴뒤($10 - 1  = 3 \times 3 $ ) 합치면 

 

$4)\ 23 \times 3 = 10 \times 7 - 1$ 이 나온다.

 

이번에는 10을 없애기 위해 1번 식에서 양변에 7을 곱하고( $125\times 7=23\times 35+10\times 7$ )

 

4번 식에서 $-1$을 좌변으로 옮긴 뒤(  $ 23 \times 3 + 1 = 10 \times 7 $ ) 합치면

 

$ 5)\ 125\times 7=23\times 38+1 $  이 나온다

 

이를 다시 정리하면 $125\times 7-23\times 38=1 $ 이 되고

 

$125x + 23y = 1$를 찾는것이 문제이기 때문에 

 

$(x, y) = (7,-38)$임을 알 수 있다.

 

$\therefore(x,y)=(7,-38)$

Extended Euclidean Algorithm 문제

이제 방법을 알아봤으니 스스로 한번 풀어보자!

 

문제 : $ 123x\equiv 1\;(mod\; 158)$일때 x의 값을 찾으시오

 

직접 풀어보고 답을 보는것을 추천한다.

 

$ 123 X\equiv 1\;(mod\; 158)$은 

 

$158\ |\ 123x-1$과 같은 의미가 된다.

 

그러므로 식을 정리하면 

 

$123x-1 = 158y$가 되고 다시 정리하면

 

$123x - 158y = 1$이라는 익숙한 형태가 나오게된다.

 

이제 유클리드 알고리즘을 적용해보자

 

$158 = 123\times 1+35$

$123 = 35\times 3+18$

$35 = 18\times 1+17$

$18 = 17\times 1+1$

 

일단 $gcd(158, 123) = 1$이므로 해가 존재하는것을 알 수 있다.

 

식을 정리하게되면

 

$123\times9 - 158\times7 = 1$이므로

 

$x = 9, y = -7$이다.

Invertible Integers Modulo N

주어진 정수 $b$에 대해 $bc\equiv 1\ (mod\ N)$인 정수 $c$가 존재하면,

 

$b$는 $N$에 대해 invertible modulo N 이라고 하며, $c$를 $b$의 multiplicative inverse 이라고 한다.

 

$b\geq 1$이고 $N > 1$이라고 가정하자. 그러면 b는 N에 대해 invertible integers일 필요충분조건은

 

$gcd(b,N) = 1$이다.

 

증명

$b$가 $N$에 대해 가역, $c$를 $b$의 역원이라 하자. 그러면  

 

$bc \equiv 1 \pmod{N} $ 즉, $bc - 1 = dN$이 성립하며, 이를 다시 정리하면

 

$bc - dN = 1$ 이다.

 

앞서 알아본 Extended Euclidean Algorithm에 따라 $\gcd(b, N) = 1$임이 성립한다.

반대로, $\gcd(b, N) = 1$이라고 가정하자. 

 

Extended Euclidean Algorithm에 따르면,

 

두 정수 $X$와 $Y$가 존재하여 $ bX + YN = 1 $이 성립한다. 

여기서 $bX \equiv 1 \pmod{N}$ 이다. 따라서 $X$는 $b$의 곱셈적 역원이다.

특별한 성질

만약 $c\ |\ ab$이고 $gcd(a,c) = 1$이라면 $c\ |\ b$가 된다.

 

그래서 만약 $p$가 소수이고 $p\ |\ ab$이면

 

$p\ |\ a$또는 $p\ |\ b$이다.

증명

$c\ |\ ab$이므로, $cd = ab$를 만족하는 어떤 정수 $d$가 존재한다.

 

만약 $\gcd(a, c) = 1$이라면, 전에 알아본 원리에 따라

 

$1 = Xa + cY$이 성립한다( $X$와 $Y$는 어떤 정수).

 

이때 양변에 $b$를 곱하면 $b = Xab + Ycb = Xcd + Ycb = c(Xd + Yb)$가 된다.

 

따라서 $c\ |\ b$가 성립한다.

Fast Powering Algorithm

만약 $3^{218}(mod\ 1000)$을 풀라고 한다면 어떻게 풀것인가?

 

먼저 제곱을 한 뒤 나눈다고 생각할 수 있지만 이 방법은 아주 느려서 사실상 불가능하다고 보아도된다.

 

그래서 이때 사용하는것이 Fast powering Algorithm이다.

 

먼저 $218$을 $2$의 거듭제곱으로 나타내면 $2+2^{3}+2^{4}+2^{6}+2^{7}$이다.

 

그러면 $3^{218}$은  $3^{2}\cdot 3^{2^{3}}\cdot 3^{2^{4}}\cdot 3^{2^{6}}\cdot3^{2^{7}}$로 표현가능한데

 

이를 각각 $mod\ 1000$하는것이다.

 

 

$3^{2^{i}}(mod\ 1000)$을 계산한것이 위의 표인데 이를 참고하여 계산하면

 

$ 3^{218}(mod\;1000)=3^{2}\cdot 3^{2^{3}}\cdot 3^{2^{4}}\cdot 3^{2^{6}}\cdot3^{2^{7}}(mod\;1000)$

$=9\cdot 561\cdot721\cdot281\cdot961(mod\;1000)$

$=489$ 임을 알 수 있다.

Chinese Remainder Theorem(CRT)

중국인 나머지정리란 $m_{1},m_{2},\cdots,m_{k}$이 쌍마다 서로소이면

 

임의의 정수열 $a_{1},a_{2},\cdots,a_{k}$에 대한 연립합동식

$x\equiv a_{1}\ (mod\ m_{1})$
$x\equiv a_{2}\ (mod\ m_{2})$
⋮
$x\equiv a_{k}\ (mod\ m_{k})$ 

 

에서 $x$가 항상 존재한다는 정리이다.

 

한번 연습문제를 풀면서 이해해보자.

 

CRT 연습문제

$x\equiv 3\ (mod\ 5)$
$x\equiv 2\ (mod\ 7)$

일때 $x$를 구하시오

 

먼저 첫번째 식은 $5\ |\ x-3$로 표현가능하므로

 

$x = 5t + 3$이 된다.

 

이를 두번째 식에 넣으면 $5t + 3 \equiv 2\ (mod\ 7)$이 이 되므로

 

이를 다시 정리하면 $15t \equiv -3\ (mod\ 7)$이 된다.

 

여기서 $15t = 14t + t$인데 여기서 중요한것이 $14t$는 $mod\ 7$을 하면 $0$이 나오는것이다!

 

그래서 $14t$는 $0$이 돼서 $t \equiv -3\ (mod\ 7)$이 된다.

 

같은 원리로 $t \equiv 4\ (mod\ 7)$가 되므로(7을 더해도 값은 변하지않음)

 

$t = 4 + 7s$가 된다.

 

이를 $x$에 관한 식에 넣으면 $x = 35s + 23$이므로

 

결국 $x \equiv 23\ (mod\ 35)$임을 알 수 있다.